1.-DIFERENCIALES:
APLICACION DE LA INTEGRAL:
APLICACION DE LA INTEGRAL:
Al integrar la diferencia entre dos funciones, puedes encontrar el área entre ellas.
No necesitamos del cálculo para averiguar el valor promedio de una función lineal en un intervalo, pero ¿qué pasa con las funciones no lineales? Afortunadamente, el cálculo integral nos ayuda aquí. En esta lección entenderemos lo que quiere decir "valor promedio" de una función en un intervalo. También relacionaremos esa noción con el teorema del valor medio que aprendimos primero en cálculo diferencial.
Valor promedio en un intervalo cerrado:
Calcular el valor promedio de una función en un intervalo
Aceleración promedio sobre intervalo:
Teorema del valor medio para integrales:
Ahora usaremos integración para encontrar la longitud de arco de una curva. Como veremos, el cálculo está basado en la misma idea de sumar un número infinito de segmentos de recta infinitesimalmente pequeños.
Desarrollo no riguroso de la fórmula de longitud de arco:
Ejemplo de longitud de arco por integración:
Otro ejemplo de longitud de arco por integración:
Otro ejemplo de longitud de arco por integración:
Ahora aprovecharemos la integral definida para hallar volúmenes de figuras donde sabemos cómo se ven los cortes transversales. Es sorprendentemente divertido.
Secciones transversales semicirculares con base triangular:
Volumen de sólido con sección transversal conocida:
2.-INTEGRAL (antiderivada)
La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
Notación
La notación que emplearemos para referirnos a una antiderivada es la siguiente:
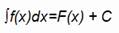
Teorema
Si dos funciones h y g son antiderivadas de una misma función f en un conjunto D de números reales, entonces esas dos funciones h y g solo difieren en una constante.
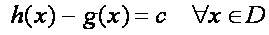
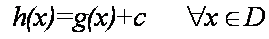
Conclusión: Si g(x) es una antiderivada de f en un conjunto D de números reales, entonces cualquier antiderivada de f es en ese conjunto D se puede escribir como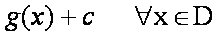 c constante real.
c constante real.
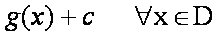 c constante real.
c constante real.
Fórmula que relaciona la integral definida y la indefinida
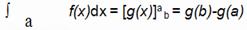
A la hora de resolver una antiderivada o integral indefinida se deben tener disponibles los recursos aritméticos y heurísticos. Estos son:
- Concepto.
- Propiedades.
- Reglas de integración.
- Integrales inmediatas.
- Métodos clásicos de integración:
-Integración por sustitución.
-Integración por partes.
-Integración de fracciones racionales mediante fracciones simples.
- Uso de tablas.
- Integración de funciones trigonométricas sencillas.
- Integración de funciones racionales sencillas.
INTEGRAL INDEFINIDA DE UN FUNCIÓN
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
 o
o 
Anti-derivadas e integrales indefinidas:
INTEGRALES INMEDIATAS:
Integrales inmediatas son las que salen directamente por la propia definición de integral, es decir, la que se puede resolver de forma más o menos intuitiva pensando en una función que cuando se derive me dé la que está en la integral.
Al igual que hicimos con las derivadas, te pongo una lista de integrales inmediatas, que como puedes comprobar es la contraria de la de las derivadas.
Otras muchas integrales, no son las que aparecen en este listado, pero difieren muy poco. Tal vez un número multiplicando o una descomposición en sumas la convierte en una de las que aparece en la tabla.
Así, para resolver una integral podemos utilizar estas dos propiedades que aparecieron en el primer vídeo:
Integral de un polinomio:
Curso integrales inmediatas.| Desde cero | 1ª parte:
Curso integrales inmediatas.| Desde cero | 2ª parte:
EJEMPLOS RESUELTOS:
Integral 1
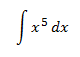
Aplicaremos la propiedad: una constante puede entrar o salir de la integral.
Multiplicaremos por la constante necesaria para tener en el integrando una derivada.
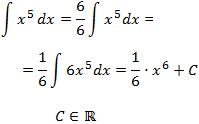
Multiplicaremos por la constante necesaria para tener en el integrando una derivada.
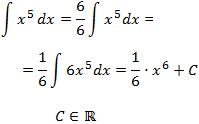
Integral 2
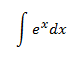
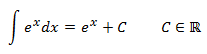
Integral 3
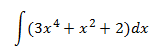
Aplicamos la propiedad: la integral de la suma es la suma de las integrales:
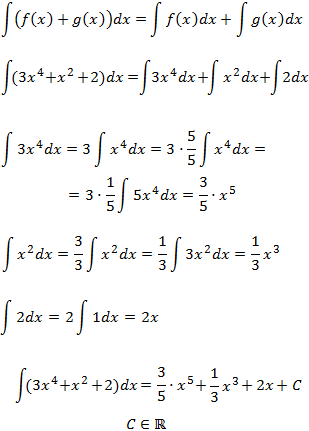
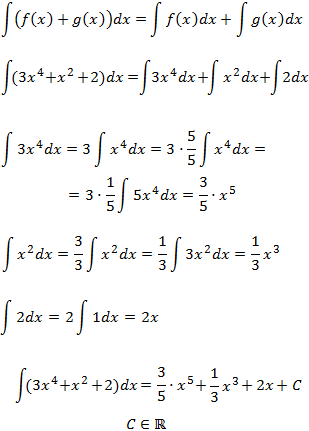
3.-Métodos de integración
Sabemos que una integral definida puede representar área y ya vimos cómo esto se conecta con la idea de una antiderivada por medio del Teorema Fundamental del Cálculo. Desafortunadamente, las integrales no siempre son fáciles de calcular. Ahora, vamos a construir nuestra caja de herramientas para evaluar integrales ¡tanto definidas como indefinidas.
Cuando quisimos sacar la derivada de f(x)g(x) en cálculo diferencial, utilizamos la regla del producto. En esta lección, vamos a utilizar la regla del producto para obtener una manera poderosa de sacar la antiderivada de una clase de funciones: la integración por partes.
Integración por partes Las funciones logarítmicas, "arcos" y
polinómicas se eligen como u.
Las funciones logarítmicas, "arcos" y
polinómicas se eligen como u.
Obteniendo la fórmula de integracion por partes:
Antiderivada de xcosx usando integracion por partes:
Integral de ln x:
Doble Integracion por partes para la antiderivada de (x^2)(e^x):
Integración por partes de (e^x) (cos x):
Integral definida periódica:
El cambio de variable es una herramienta imprescindible en cualquier arsenal de integración (por lo general las herramientas no se guardan en arsenales, pero eso suena mejor que caja de herramientas). En esencia, es el inverso de la regla de la cadena. Podría usarse cualquier letra, pero por convención se suele usar la letra "u".
Sustitucion U:
Cambio de variable. Ejemplo 2:
Sustitución (U) con una función exponencial:
Cambio de variable y sustitución de regreso:
Otra técnica muy útil para calcular integrales involucra reemplazar variables con funciones trigonométricas. Esto puede hacer que las cosas parezcan un poco complicadas al principio, pero con la ayuda de las identidades trigonométricas, esta técnica hace que podamos resolver ciertas integrales.
Introducción a la sustitución trigonométrica:
Integrales Sustitución trigonométrica 1:
Sustitución trigonométrica y cambio de variable juntas (parte 1)
Sustitucion U y trigonometrica juntas (Parte 2):
Cuando estás tratando de integrar una expresión racional, las técnicas de desarrollo en fracciones parciales y división larga de polinomios pueden ser *muy* útiles.
Fracciones parciales para evaluar la integral:Cuando estás integrando una función que tiene la forma de una fracción, es útil encontrar una manera de separar la expresión.
Dividiendo expresiones para evaluar integral:Aquí hacemos división larga de polinomios para hacer más fácil el cálculo de una integral.
4.-INTEGRAL DEFINIDA
Dada una función f(x) y un intervalo [a,b], la integral definida es
igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las
rectas verticales x = a y x = b.
La integral definida se
representa por 
∫ es
el signo de integración.
a límite
inferior de la integración.
b límite
superior de la integración.
f(x) es
el integrando o
función a integrar.
dx es diferencial de x, e indica
cuál es la variable de la función que se integra.
El cálculo diferencial se basa principalmente en razones de cambio. Esto es, después de todo, lo que son las derivadas. Como veremos, el cálculo integral se basa principalmente en sumar o "integrar" un número infinito de cosas infinitesimalmente pequeñas, para así obtener un valor finito. Frecuentemente, este valor representa el área bajo una curva. Esta lección es un anticipo de la conexión entre estos dos conceptos.
Área bajo la función de razón de cambio:
En esta lección, pensaremos en cómo podemos encontrar el área bajo una curva. Primero la aproximaremos con sumas de áreas de rectángulos (y de trapecios) —generalmente llamadas sumas de Riemann
Introducción a la aproximación de Riemann:Aproximar el área bajo una curva al sumar el área de rectángulos. A esta aproximación se le llama "suma de Riemann"
Aproximación de Riemann simple usando rectángulos:
Generalizando una suma de Riemann izquierda con rectángulos equiespaciados:Generalización de la técnica de aproximación del área bajo una curva por medio de rectángulos.
Sumas de Riemann e integrales:El momento que estabas esperando. En esta lección establecemos la conexión entre las sumas de Riemann y las integrales.
INTEGRAL DEFINIDA (VOLUMEN)
El volumen del cuerpo de revolución engendrado al girar la curva f(x) alrededor del eje OX y limitado por x = a y x = b, viene dado por:
Ejemplos
1. Hallar el volumen del tronco de cono engendrado por la rotación alrededor OX del área limitada por y = 6 − x, y = 0, x = 0, x = 4.
2. Calcular el volumen engendrado por una semionda de la sinusoide y = sen x, al girar alrededor del eje OX.
3. Hallar el volumen del cuerpo revolución engendrado al girar alrededor del eje OX, la región determinada por la función f(x) = 1/2 + cos x, el eje de abscisas y las rectas x = 0 y x = π.
4. Hallar el volumen engendrado por el círculo x2 + y2 − 4x = −3 al girar alrededor del eje OX.
El centro de la circunferencia es C(0, 1) y el radio r = 1.
Puntos de corte con el eje OX:
5. Calcular el volumen engendrado al girar alrededor del eje OX el recinto limitado por las gráficas de y = 2x − x2, y = −x + 2.
Puntos de intersección entre la parábola y la recta:
La parábola está por encima de la recta en el intervalo de integración.
ELABORADO POR:
IBC
JE
GLT
BA